Induction

A look at mathematical induction

Introduction

The most interesting and complex puzzles we as humans can describe are defined in advanced mathematics Worth noting that this is a personal opinion not a fact . We tackle these puzzles using the axiomatic systems of mathematics and logical language defined by proof theory. It is proof theory that I am reviewing right now in an attempt to improve my understanding of certain proofs in topology. In particular that of induction caught my interest Enough to write a paper about it anyway. . The model of proof known as induction is not unique to mathematics, It has been used in philosophy as a kind of argument strategy in an obscured fashion. In particular there exists a philosopher that used induction both as a philosophical argument strategy and mathematical device (see the section on Gersonides). There seems to be a conflict in generality between the mathematical induction and the philosophical induction math and philosophy have different levels of rigor as one might suspect. . Here I will to focus solely on the mathematical method of proof, as the philosophical equivalent seems less rigorously defined.

Proof by Induction

Learning from a book has always come easiest to me and my favorite book describing this subject would have to be . I have (re)learned the technique of proof by induction three different times now: in undergrad, for my thesis work, for fun. Each time I review the material it seems to give me a different understanding of induction. This is possibly effected by my using different (possibly better) material to learn each time. In undergrad I had a more naive notion that was induction was the process by which you proved some hypothesis over some recursively ascending system. Now my favorite way to understand induction is through the use of a Peano model. In particular as long as there is some set containing an identity and some notion of a successor, one could theoretically use induction. The use cases under the latter understanding are vastly increased. Note I am not claiming that my abstract understanding is the best one, its simply better than my previous understanding. In mathematical induction one creates a hypothesis using some simplified version of the proposition. We then prove some base case of this hypothesis, whence we can insert the hypothesis into some inductive proof as a tool to simplify the algebra This is not a perfect explanation, I apologize if the reader should be mathematician..

\[\begin{equation} \label{weak_induction} \begin{split} \text{Prop 1: }& \\ &2 + 4 + 6 + \dots + 2n = n(n+1) \\ \text{Inductive Hypothesis}& \\ &2 + 4 + 6 + \dots + 2n = n(n+1) \\ \text{Base Case}& \\ &n = 1, 2 = 1(1+1) \\ \text{Inductive Step}& \\ &2 + 4 + 6 + \dots + 2n + 2(n+1) = (n+1)((n+1)+1) \\ &n(n+1) + 2(n+1) = (n+1)(n+2) \\ &n^2 + 3n + 2 \triangleq n^2 + 3n + 2 \\ \end{split} \end{equation}\]

An elementary use of this technique can be see in Eq \eqref{weak_induction}. This proof shows that induction can be used to prove the general formula for a series. In general induction can prove some proposition for a series on the order of natural numbers. This means that any set indexable via the natural numbers can utilize induction to prove a proposition across the set as a whole. In particular if one can prove a base case then one must only prove that the proof of a step $k$ implies the proof of the step $k+1$. This is ascending induction as apposed to descending induction (or Fermatian induction, see the section on Fermat). In general a proof by induction has this form: where one must prove a base case $P_1$; then a hypothesis (general form) $P_k$; then prove the step $P_{k+1}$ (see pg. 149 for a brilliant diagram).

Of course The form above is not the only form of induction. In particular there are many forms the inductive technique can take on. Complete induction or strong induction is described as utilizing all past steps (past proofs) at each current step. There also exist proofs which utilize the nature of mathematical induction without following the structure, such as Peano’s design of the natural numbers (See the Peano section).

History of Mathematical Induction

It is evident from research presented that the exact inventor of the mathematical induction method is debated. Each usage is both innovative and exciting given the notational boundaries of the times. In particular I find Pascal’s arithmetic triangle to be extremely interesting, has given me an understanding of the triangle that would have been impossible to acquire previous to their paper. It is impossible to truly see the value in a technique if one does not understand why it was invented, thus it becomes imperative to investigate the history of powerful methods I do not find this to be controversy, if that is the case then this is simply my opinion.. The process by which I selected the below individuals to discuss is by interest. Interest can take multiple forms as listed below.

Disadvantage: some of the proofs take place when math tools where disadvantageous.
Innovation: there are proofs that display a level of unique inspiration such as the arithmetic triangle and construction of natural numbers.

There is of course the possibility that a particular proof had some semantic interest for me. Such as a personal interest in philosophy biasing my use of Gersonides as an example of induction. Here I examine a selected few inventors (or first user) of induction and their influence on the method. Note the use of subsections below as primers for esoteric information.

Maurolycus

Born in the late thirteenth century Francesco Maurolico is not only a talented mathematician, but the master of mint, head architect of defences, and a professor in Sicily. For the remainder of this paper I will use the Latin translation of his name Maurolycus as this is the version used by historic mathematicians. It is said by Bussey in that Georg Cantor named Maurolycus as using the proof technique of induction first. The exact quote used by Bussey from Cantor:

Mr. G. Vacca pointed out that Maurolycus had already described the method in detail and used it in his Arithmetic of 1575. However, Pascal was the first to take it from Maurolycus. There can be no doubt about this, since in 1659 Pascal explicitly cited Maurolycus, who had proved this very theorem by means of complete induction. (translated from German to English)

\begin{equation}\label{maurolycus_simple} 2 (\frac{n(n+1)}{2}) - n = n^2 \end{equation}

Here Cantor makes reference to Eq \eqref{maurolycus_simple} that was in a Pascal article siting Maurolycus. A rigorous examination of work by Maurolycus is present in . In particular it is noted that Pascal may have gleaned the knowledge of complete induction from Maurolycus’s writings .

Gersonides

An interesting and rather isolated theory from is that induction was first used by Rabbi Levi ben Gershon. Better known as his Greek-translated name Gersonides; Levi ben Gershon is a French-Jewish philosopher from the early fourteenth century. Work from Gersonides is presented in pointing to his use of induction in the proof of mathematical theorems. In particular proposition 63 of the Maasei Hoshev which describes a method of determining the number of permutations of sets.

Proposition 63: [Let] the number of permutations of a given number of different elements be some fixed number, $P_n$ then the permutations of a set of different elements numbering one more than the given number are as many as the product of the former number of permutations by the successor to the given number.

While the proof of this proposition is not provided it is stated that the use of induction is “implied”. In particular the definition of proof by induction is weakened, stating that older proofs often used “quasi general” inductive techniques. Demonstrated with proofs that only worked for select or special cases This seems normal to me as theorems start by examining special cases then becoming more general over time.. If these quasi general processes are used knowingly it is not made obvious to the reader in . In fact there is indication that the quasi general induction is a symptom of older notation. The notation used by Gersonides for instance is not powerful enough to represent sequential elements of a set abstractly.

\[\begin{equation} \label{eq:modern-note} \begin{split} S &\leftarrow \{ 0,1,2,3,4,5, \dots \}, \quad n &\in \mathbb{N} \\ S_n &\in S \implies S_{n+1} \in S \end{split} \end{equation}\]

We see in equation \eqref{eq:modern-note} our notation is powerful enough to define a set and then define unique elements of that set abstractly. This is seen in $S_n$ representing some nth element of the set $S$. Knowing that $S$ is the set $\mathbb{N}_0$ no good argument has been brought to me presenting the natural numbers as including zero thus $\mathbb{N_0}$ is the set of natural numbers with the edition of zero. this implies $S_{n+1}$ is the subsequent element to $S_n$ which by definition is included in $S$.

The same statement in the notation Gersonides is described using is thus.

\[\begin{align*} &\text{Given a set $S$ such that it contains the natural numbers and zero.} \\ &\text{We can infer that any element $m$ of this set $S$ has a subsequent element $n$ also contained in $S$.} \end{align*}\]

The idea of abstracting the elements of sets into ordered, indexable space such as $S_0, S_1, S_2$, came later. In particular in the writings of Gersonides each element in question required a unique identifier such as $m$ or $n$. It is obvious why this would become cumbersome during a procedure such as induction. Thus describes the methods used as inductive in nature regardless of their quasi generality. We see in that Maurolycus reviewed Gersonides work stating:

With great liberality, the procedure may perhaps be called complete induction, although the peculiar formal structure of complete induction is missing (translated using Google translate)

This is to say that Gersonides technique of “rising step-by-step” or Hadragah is similar to the structure of complete induction as a recursive process. In particular Hadragah is demonstrably proving that given the proof of an index $S_n$ it implies the subsequent index $S_{n+1}$ can be proven, without the rigorous structure of complete induction.

Pascal

Blaise Pascal is a mathematician from the mid seventeenth century . The inventor of Pascals triangle which explores different orders of figurate numbers, that is orders of binomial coefficients . It is in the paper Trait ́e du triangle arithm ́etique that we find Pascal using the technique of complete induction . I would be remiss not to explore Pascals triangle, thus allow me a tangent here to describe the genius that is Pascals triangle.

The Triangle

The structure itself is well known although some of the intricacies eluded either my memory or my education. The triangle is designed to describe figurate numbers.

[F]igurate numbers count the number of dots in regularly shaped figures, such as line segments, triangles, pyramids, etc.

It is these numbers that form what Pascal refers to as “orders” of numbers and we describe as dimensions. Figurate numbers can be found in any dimension ($lim_{0\to\infty}$), thus requiring a recursive definition. We can describe the first three orders here.

Numbers of the first order represent the dots of a shape in a single dimension and thus are all a unit or $\{1,1,1,1,1, \dots \}$
Numbers of the second order represent the dots of a shape in two dimensions and thus are the natural numbers $\mathbb{N}$
Numbers of the third order represent the dots of a shape in three dimensions and thus are the triangular numbers $\{1,3,6,10, \dots \}$

Pascals triangle describes all of these in a recursive definition dependent on the structure of the triangle and the generator. In particular the generator is the first number inserted into the triangle that will act as the value of the unit. All other numbers of the triangle are a sum of the numbers preceding them either row or column independent. We can describe any index of the triangle as a cell. In particular we can think of all these cells in the structure of a matrix. Thus the formula for creation of each new cell ($C$) is described by Eq \eqref{pascal_formula}.

\[\begin{equation} \label{pascal_formula} \begin{split} C_{n,m} &= \text{Generator} &\mid (n = 0) \land (m = 0) \\ C_{n,m} &= A_{n-1,m} + B_{n,m-1} \quad &\mid (n > 0) \lor (m > 0) \end{split} \end{equation}\]

Use of induction

Returning to our original point that Pascal used complete induction to prove that the formula for his triangle would always create figurate numbers. The evidence for this can be found in Pascals twelfth consequence. In particular the twelfth consequence states precisely that the triangle will always produce figurate numbers. In the treatise mentioned above Pascal described consequences of the triangle, these are better thought of today as intricacies of his triangle. In fact the first few consequences (namely one through three) seem to state the obvious. In the twelfth consequence described in , Pascal forms a proper complete induction structure based around the relation of certain elements.

In every arithmetical triangle, of two contiguous cells in the same base the upper is to the lower as the number of cells from the upper to the top of the base is to the number of cells from the lower to the bottom of the base, inclusive.

Pascal refers to a base here as a subset of numbers within the triangle itself. For more clarity I have included an image of pascals triangle below, taken from .

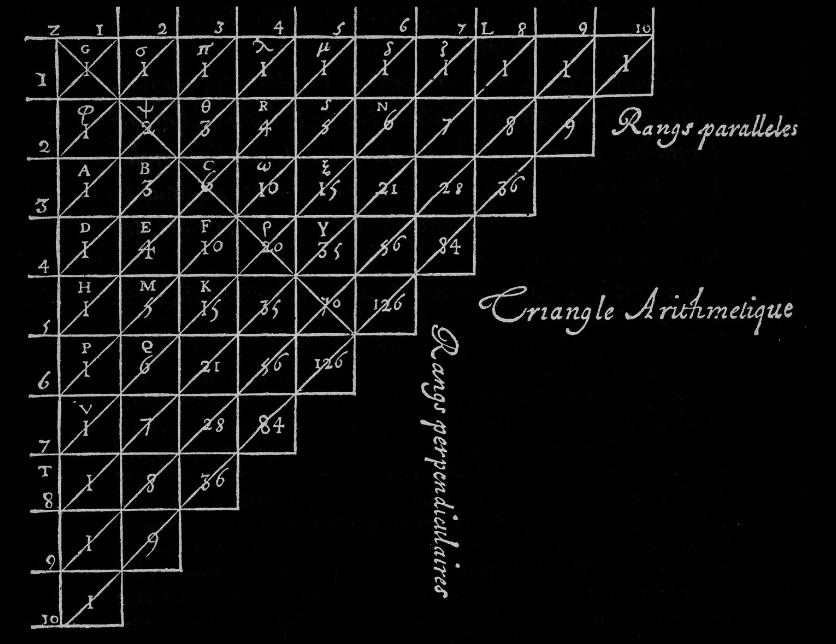
In Pascals triangle we can see a diagonal set of lines from one extrema to another. A single example of this line can be seen in the line $\lambda , D$, This line is describing a single base. In particular for the base described by $\lambda, D$, its contents are shown as $\{ D, B, \theta, \lambda \}$. Thus Pascal is stating that the relation between any two contiguous elements of a single base is dependent on their distance from their respective extrema.

\[\begin{equation} \begin{split} A = \{ D, B, \theta, \lambda \} \\ B : \theta \triangleq 1 : 1 \end{split} \end{equation}\]

This makes sense given that $B$ & $\theta$ are reciprocals, values Pascal describes as always being equal. With a similar example Pascal’s base case is proven. The next step is somewhat tricky as one must assume something not so obvious (the tool of complete induction). He goes on to say that the rule follows in the next base (an obvious truth). Then he states that necessarily if the rule is true at any base, it must be true at its successor.

[T]hat if this proportion is found in any base, it will necessarily be found in the following base.

This supposes that if one can prove that its true for some base $x$ then it will by definition be true for all subsequent bases of $x$. The final pieces of the proof are predictable and unimportant to this paper, as it discourages you from reading .

Peano

Giuseppe Peano demonstrates a much more interesting use of mathematical induction. The creation of axioms for the natural numbers, utilizing the inductive principle that underpins all of the above proofs. In the proofs we have spoken of thus far, all share in common the concept of successor and identity element that is crucial to mathematical induction. In particular there is some base case (identity) from which the hypothesis is demonstrated, then applied to the successors in a kind of $A \implies B \implies C \dots$ fashion. These represent the most basic of assumptions underlying induction which even apply to Gersonides quasi-general induction. My interest in Peano’s use of induction is that there is not much left to assume. Peano utilizes the idea of successor, identity, and some basic set theory to prove the theory of natural numbers Given he does include "zero" in his model for natural numbers but lets forgive him for that. . Peano utilizes the inductive technique in his rigorous defining of the natural numbers, along with set theory and first order logic. The corner stone of Peano’s definition is the Peano model, a triple built of natural number, zero (or an identity), and a successor. This model presupposes only logic and elementary set theory to be defined rigorously. An example of the model can be seen in Eq \eqref{peano_model_example}, where the successor is seen as a unary function producing the successor of its input.

\[\begin{equation} \label{peano_model_example} \langle N, 0, S \rangle \end{equation}\]

Peano model

In the interest of time I have included all the axioms to this model at once, in addition to rewriting older portions of logic in modern latex It was not my intent to change the logic of Henkin, though some of the symbols in the paper are difficult to make out.. The complete list of axioms defining the Peano model are shown in Eq \eqref{peano_axioms}.

\[\begin{equation} \label{peano_axioms} \begin{split} \text{Axiom 1:}& \quad \forall x \in N, S(x) \neq 0 \\ \text{Axiom 2:}& \quad \forall x,y \in N, x \neq y \implies S(x) \neq S(y) \\ \text{Axiom 3:}& \quad G \subset N \mid (0 \in G) \land (x \in G \implies S(x) \in G), \implies G = N \\ \text{Axiom 4:}& \quad y \in N \mid y \neq S(x), \forall x \in N \implies y = 0 \\ \text{Axiom 5:}& \quad \forall x \in N, x \neq S(x) \\ \end{split} \end{equation}\]

Axiom one states that for any number of the set $N$ the subsequent number defined by the function $S$ can never be the identity (zero). The reason I make the distinction of identity to zero is that one can use this model elsewhere to define a set of numbers where the identity is not zero. In particular I sense similarities between Peano models and the most basic of topological sets, with the obvious absence of the triangle axiom whether or not this similarity is founded in reality or hallucination is up for debate.. Axiom two describes the successor function as injective, that is for each unique element of the set $N$ there will be a unique successor. Axiom three describes equality between different model sets. In particular if a set $G$ includes both the identity and successor of all its elements implies that it is equivalent to the Peano model set $N$. Axiom four defines a rule where the only element of $N$ with no successor must be the identity element (zero). Axiom five makes obvious that by the definition of the successor function no element of $N$ can be equivalent to its successor. Note these Axioms hold only for the Peano model. In particular describes that there exist arbitrary models using permutations of this axiom set, these are not Peano models.

It is now appropriate to describe the interesting use of induction to this axiomatic definition of natural numbers. Peano defines his model to include a set of numbers (natural numbers), an identity, and a successor function. Using these he rigorously defines the natural numbers, using a base case (the identity) and defining that all axioms hold for all successors of that base case. It is not (entirely) wrong to say that Peano used the technique of induction to design his rigorous model for natural numbers. In particular without the techniques of induction it is not obvious to me that this rigorous definition is possible.

Nomenclature

$\leftarrow \quad $ The symbol for assignment, $S \leftarrow {0,1,2}$ means that $S$ is the name for the set ${0,1,2}$
$\triangleq \quad $ The symbol for equals by definition, thus $0 \triangleq 0$ by the laws of arithmetic this statement must be true.
$\forall \quad $ The symbol for for all, thus $\forall x \in S$ means that $x$ will take the value of all elements of the set $S$.
$\implies \quad $ The symbol for implies, thus $P_1 \implies P_2$ means that should $P_1$ be true then $P_2$ is true.
$\in \quad $ The symbol is contained in, thus $n \in N$ means that the value $x$ is contained in the set $N$.
$\mid \quad $ The symbol for such that, thus $n \in N \mid n = 5$ means that $n$ is a value contained in $N$ such that $n$ is the number $5$.
$\land \quad $ The symbol for logical and, thus $P_1 \land P_2$ both $P_1$ and $P_2$ must be true if the statement as a whole is to be true.
For my fellow computer scientists, in this post I begin counting from zero as a mathematician would.
$S(x) \quad $ This is to symbolize the function $S$ taking as an input the value $x$.
$M_{a,b} \quad $ Here $M$ symbolizes a matrix where $a$ and $b$ are indexing that matrix in row, column style.
$\lor \quad $ This is the symbol for logical or, thus $P_1 \lor P_2$ this statement is true if $P_1$ or $P_2$ is true.